시작은 제일제당이 맨날 실적 발표 전에 올랐다가, 발표하면 내려가는 거 같고, 이번엔 달라! 하면 귀신같이 떨어지니까
하... 이럴 바에는 그냥 오르면 팔고 다시 내려가서 살걸...
이라는 생각에서 출발하였다.
원래 계획은
"수익률이 정규분포라면, \( \pm 2 \sigma\) 범위가 정상 등락폭이라고 보고, 주가 변동이 + 2\(\sigma\)위로 가면 팔고, -2\(\sigma\) 아래로 가면 사야겠다."였다.
다음 코드는 R에서 작성되었다.
> cjcheil <- read.csv("stockdata/cj제일제당.csv")
> str(cjcheil)
'data.frame': 3464 obs. of 11 variables:
$ 일자 : chr "2021/10/01" "2021/09/30" "2021/09/29" "2021/09/28" ...
$ 종가 : int 401000 409500 410500 416500 429000 430000 432500 431000 429500 435000 ...
$ 대비 : int -8500 -1000 -6000 -12500 -1000 -2500 1500 1500 -5500 -6000 ...
$ 등락률 : num -2.08 -0.24 -1.44 -2.91 -0.23 -0.58 0.35 0.35 -1.26 -1.36 ...
$ 시가 : int 407000 409500 411000 427000 428500 431500 430500 429500 435000 438000 ...
$ 고가 : int 410500 413500 417000 428000 436500 433500 434500 433000 437500 442500 ...
$ 저가 : int 397000 405500 404000 414500 427500 428000 426000 427000 428000 434000 ...
$ 거래량 : int 59272 31515 51544 44231 25407 19143 32735 42846 46630 43530 ...
$ 거래대금 : num 2.37e+10 1.29e+10 2.11e+10 1.86e+10 1.10e+10 ...
$ 시가총액 : num 6.04e+12 6.16e+12 6.18e+12 6.27e+12 6.46e+12 ...
$ 상장주식수: int 15054186 15054186 15054186 15054186 15054186 15054186 15054186 15054186 15054186 15054186 ...
데이터를 다운로드 받아서 보면, 일자가 날짜가 아닌, chr형식으로 된 것을 확인할 수 있다.
얼른 날짜로 변환해주자.
library(lubridate)
cjcheil$일자<- ymd(cjcheil$일자)
lubridate 패키지의 ymd함수를 사용했다. ymd는 이름에서 볼 수 있듯, "year-month-day" 순서로 입력된 데이터를 날짜로 변환해주는데 구분자에 관계없이 인식해준다는 장점이 있다.
다른 형태로도 적용이 되는데 2021-28,11"이면 ydm, "05-11-2021"이면 mdy 등,
데이터 포맷이 변해도 이에 맞춰서 함수를 바꿔서 적용해주면 된다. 개꿀함수 ㅎㅎ
ydm <- c("2021,28,11")
> str(ydm)
chr "2021,28,11"
ydm<- ydm(ydm)
> str(ydm)
Date[1:1], format: "2021-11-28"
mdy<- c("05,11-2021")
> str(mdy)
chr "05,11-2021"
mdy<- mdy(mdy)
> str(mdy)
Date[1:1], format: "2021-05-11"
아래 작업은 tidyverse를 이용하여 진행하였다.
library(tidyverse)
-- Attaching packages ------------------------------------------------------------------------ tidyverse 1.3.1 --
√ ggplot2 3.3.5 √ purrr 0.3.4
√ tibble 3.1.3 √ dplyr 1.0.7
√ tidyr 1.1.3 √ stringr 1.4.0
√ readr 2.0.1 √ forcats 0.5.1
-- Conflicts --------------------------------------------------------------------------- tidyverse_conflicts() --
x dplyr::filter() masks stats::filter()
x dplyr::lag() masks stats::lag()
우선 코스피 지수와 제일제당의 주가 그래프를 그려봤다.
ylim.fir <- c(0,4000)
ylim.sec <- c(100000,500000)
b <- diff(ylim.fir)/diff(ylim.sec)
a <- ylim.fir[1] - b*ylim.sec[1]
# 코스피랑 제일제당이랑 범위 차이가 나서 축 조정
ggplot(data = KOSPI %>% filter(일자>="2007-09-28")) +
geom_line(aes(x=일자, y=종가),colour="black",size=0.8)+
labs(x="",y="",title="KOPSI INDEX")+
scale_x_date(date_breaks="3 year")+
scale_y_continuous("KOSPI", sec.axis = sec_axis(~ (. - a)/b, name = "CJ제일제당"))+
geom_line(data=cjcheil,aes(x=일자,y= a + b*종가),colour="red3",size=0.8)+
theme_bw()+
theme(axis.text = element_text(size=8),
axis.title.y = element_text(size=16),
axis.line.y.left = element_line(color = "gray25"),
axis.ticks.y.left = element_line(color = "gray25"),
axis.text.y.left = element_text(color = "gray25"),
axis.title.y.left = element_text(color = "gray25"),
axis.line.y.right = element_line(color = "red4"),
axis.ticks.y.right = element_line(color = "red4"),
axis.text.y.right = element_text(color = "red4"),
axis.title.y.right = element_text(margin=margin(0,0,0,6),color = "red4")
)

위와 같은 그래프가 나타났다.
"아 이거 생각을 잘해야겠다. 첨에 생각한 데로 하면 잘못하면 칼날에 사서 저점 반등에 팔겠네..."
라는 교훈을 얻을 수 있는 그래프였다.
둘의 움직임은 비슷한 모습을 보이는 듯.
다음은 등락률의 히스토그램을 살펴보았다. 정규성 확인은 역시 히스토그램이지~
ggplot(data=cjcheil, aes(x=등락률))+
geom_histogram(colour="black",alpha=0.5)+
geom_freqpoly(colour="black",size=1.5,alpha=0.7)+
labs(x="",y="",title="일별 등락률")+
theme_bw()
어 뭔가 이상하다. 너무 뾰족한 듯.
정규분포랑 비교해 볼까
ggplot(data=cjcheil, aes(x=등락률))+
geom_density(size=1.5,colour="black",alpha=0.3)+
stat_function(fun = dnorm,args = list(mean=mean(cjcheil$등락률),sd=sd(cjcheil$등락률)),colour="red",size=1.5,alpha=0.5)+
theme_bw()+
labs(x="일별 등락률",y="",title="일별 등락률의 밀도함수 vs 정규분포",caption="밀도함수 검정, 정규분포 빨강")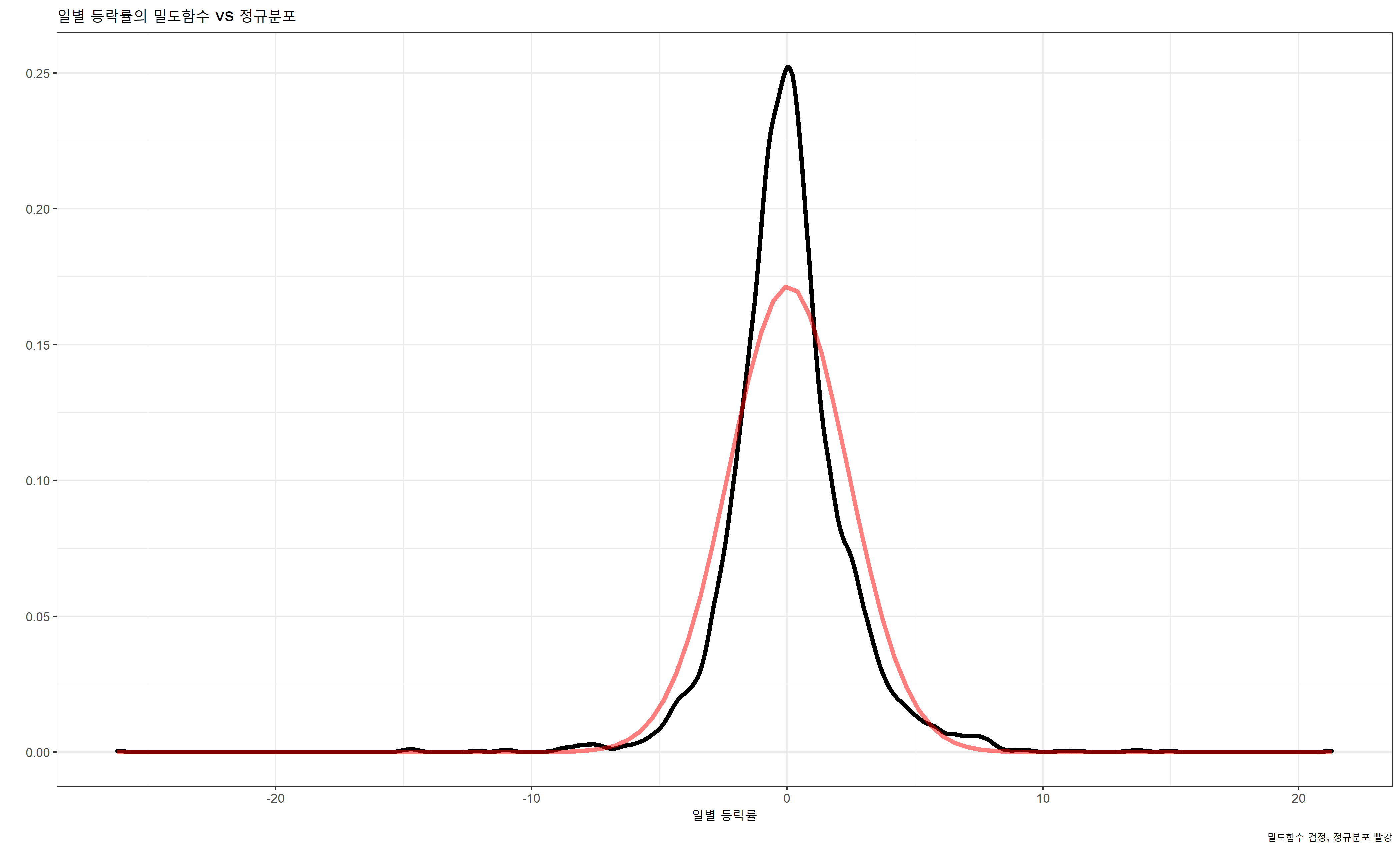
어... 정규성 검사...
ggplot(data = cjcheil, aes(sample=등락률))+
stat_qq()+
theme_bw()
> shapiro.test(cjcheil$등락률)
Shapiro-Wilk normality test
data: cjcheil$등락률
W = 0.91909, p-value < 2.2e-16
아니란다! 해서 약간 멘붕이 왔지만, 근데 내가 뭐 통계 분석할 것도 아니고 정상 범위 비정상 범위 나누는 데에 큰 의미는 없다고 생각해서 그냥 마저 하기로 했다.
ggplot(data=cjcheil, aes(x=등락률))+
geom_density(size=1.5,colour="black",alpha=0.3)+
stat_function(fun = dnorm,args = list(mean=mean(cjcheil$등락률),sd=sd(cjcheil$등락률)),colour="red",size=1.5,alpha=0.5)+
geom_vline(aes(xintercept=mean(등락률)+ 2*sd(등락률)),linetype = "dashed", colour="red",size=0.8, alpha=0.5)+
geom_vline(aes(xintercept=mean(등락률)- 2*sd(등락률)),linetype = "dashed", colour="red",size=0.8, alpha=0.5)+
theme_bw()+
labs(x="일별 등락률",y="",title="일별 등락률의 밀도함수 vs 정규분포",caption="밀도함수 검정, 정규분포 빨강")
실제로 \(\pm 2\sigma\)가 되는 구간 점선으로 표시해보니 그냥저냥 비슷해 보인다. 일단 해보자고~
'코딩' 카테고리의 다른 글
| 제일제당, 존버가 답이었을까? - 5편 (0) | 2021.10.23 |
|---|---|
| 제일제당, 존버가 답이었을까? -4편 (0) | 2021.10.20 |
| 제일제당, 존버가 답이었을까? - 3편 (0) | 2021.10.10 |
| 제일제당, 존버가 답이었을까? -2편 (0) | 2021.10.09 |
| 제일제당, 존버가 답이었을까? - 0편 (0) | 2021.10.08 |


